Buying a heat pump the data scientist way
Context
The Summer of 2018 was ridiculously hot and we decided that we wanted to buy a central air conditioning unit. Would spending more to get an air-air heat pump instead make economic and environmental sense?
a quick note: shopping for heat pumps sucks. Every salesman claims to have the best reliability and service, and there is no independent source that will help you sort it out.
A quick introduction to heat pumps
The air-to-air heat pump is an amazing device.
During the Summer it operates like any air conditioning device, transferring heat from the air inside the house to the air outside. During the Winter, it reverses it’s operation and efficiently transfers the heat from the (cold) air outside to the warm air inside my house.
The efficiency of the heat pump is measured by it’s coefficient of performance (COP), which measures how many kWh of heat will be added to my house for each kWh of electricity used by the pump. For Energy Star rated heat pumps, the COP hovers between 2 and 4 depending on the outside temperature. The closer the outside temperature is to the inside temperature, the higher the efficiency.
As a comparison, electric furnace and electric baseboard are 100% efficient at converting electrity to heat, which means they have a a COP of 1. Heating systems based on burning stuff are less than 100% efficient since some heat escapes through the chimney, achieving COPs between 0.6 and 0.9.
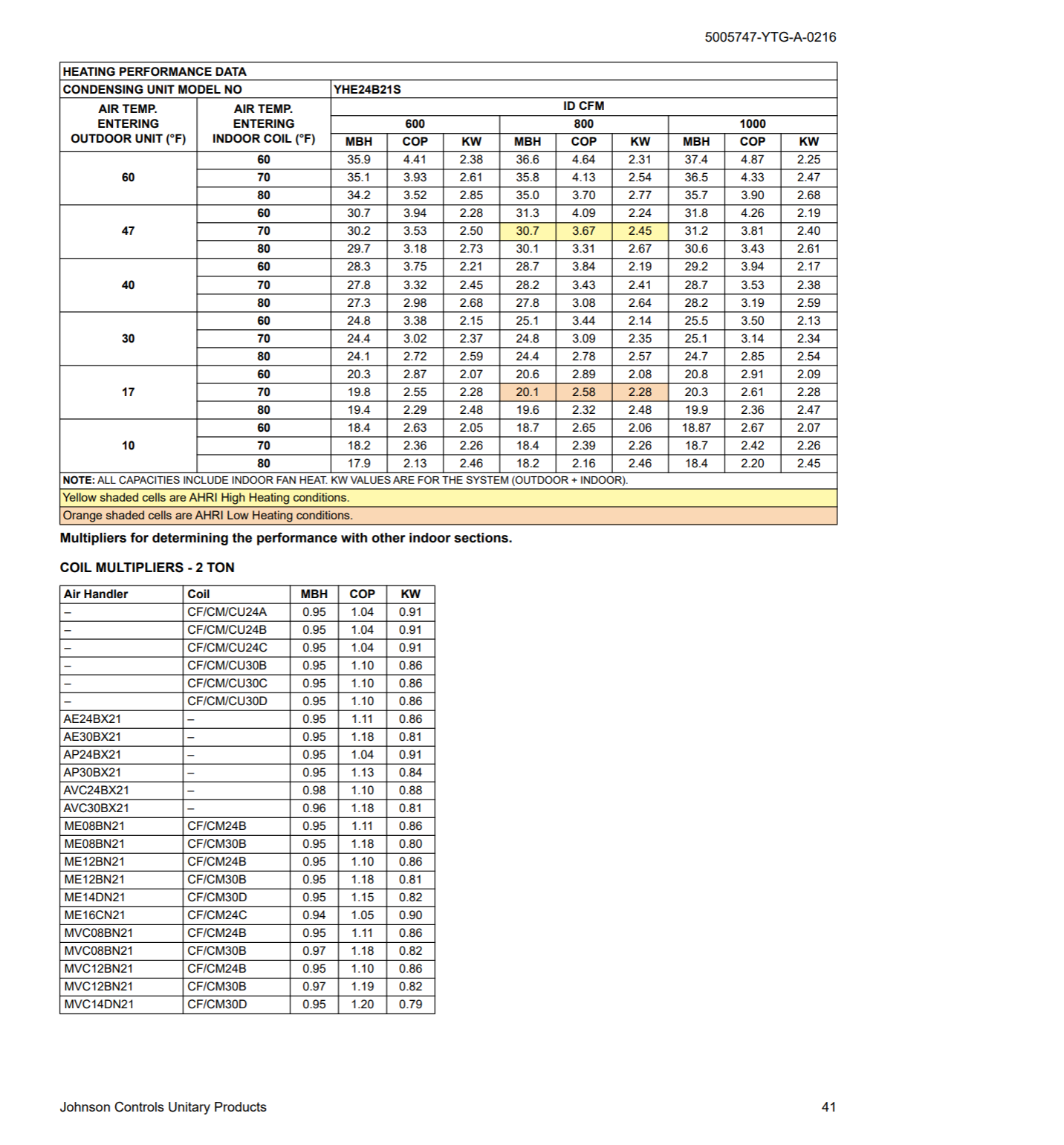
The capacity of the heatpump measures how much energy it can transfer to the house over a period of time. A COP of 4 isn’t impressive if the pump is only able to multiply the energy output of a single candle by 4, as that won’t be enough to heat my house during winter. The capacity of most heat pumps generally falls dramatically around -12C, with the Mitsubishi Zuba being a very expensive outlier.
In Canada, the capacity of heating systems is measured in MBH, where 1 MBH is 1000 Btu/h. 1 kW is equivalent to 3.41 MBH.
It is complicated to compare the efficiency of different heat pumps because their COP varies with the temperature. Heat pump “A”" could have a higher COP than Heat pump “B”" at 10C, while the opposite could be true at 5C. To simplify comparisons, the technical sheets typically include the Heating Seasonal Performance Factor (HSPF), which is a form of seasonnally-adjusted COP for a specific climate. The HSPF is defined as the ratio between the MBH output and the kWh input, so if you want the ratio of kWh input to kWh output you have divide it by 3.41.
I am considering purchasing the York YHE24B21S central heat pump with a CF24BXA1 coil and a ME12BN21 air handler.

This setup has a published HSPF of 8.50 in region 4, which is equivalent to a HSPF of 7.391 in region 5. Dividing by 3,41, we obtain an average COP of 2.16, meaning that the heatpump should divide your heating bill by 2.16 in region 5. Region 5 has a climate equivalent to the city of Ottawa. Quebec City is colder on average, which means the system should also be less efficient on average.
A house heated with a heat pump has to have a backup system. In my case, the backup system is an electric furnace. There are two reasons to shift from the heat pump to the backup system:
- As the outside temperature drops, the COP will also drop and will eventually reach a point where you the heat pump isn’t more efficient than your backup system. At that point, you should switch to your backup system to reduce wear and tear. I don’t remember the source, but I read somewhere that switching around a COP of 1.5 makes sense.
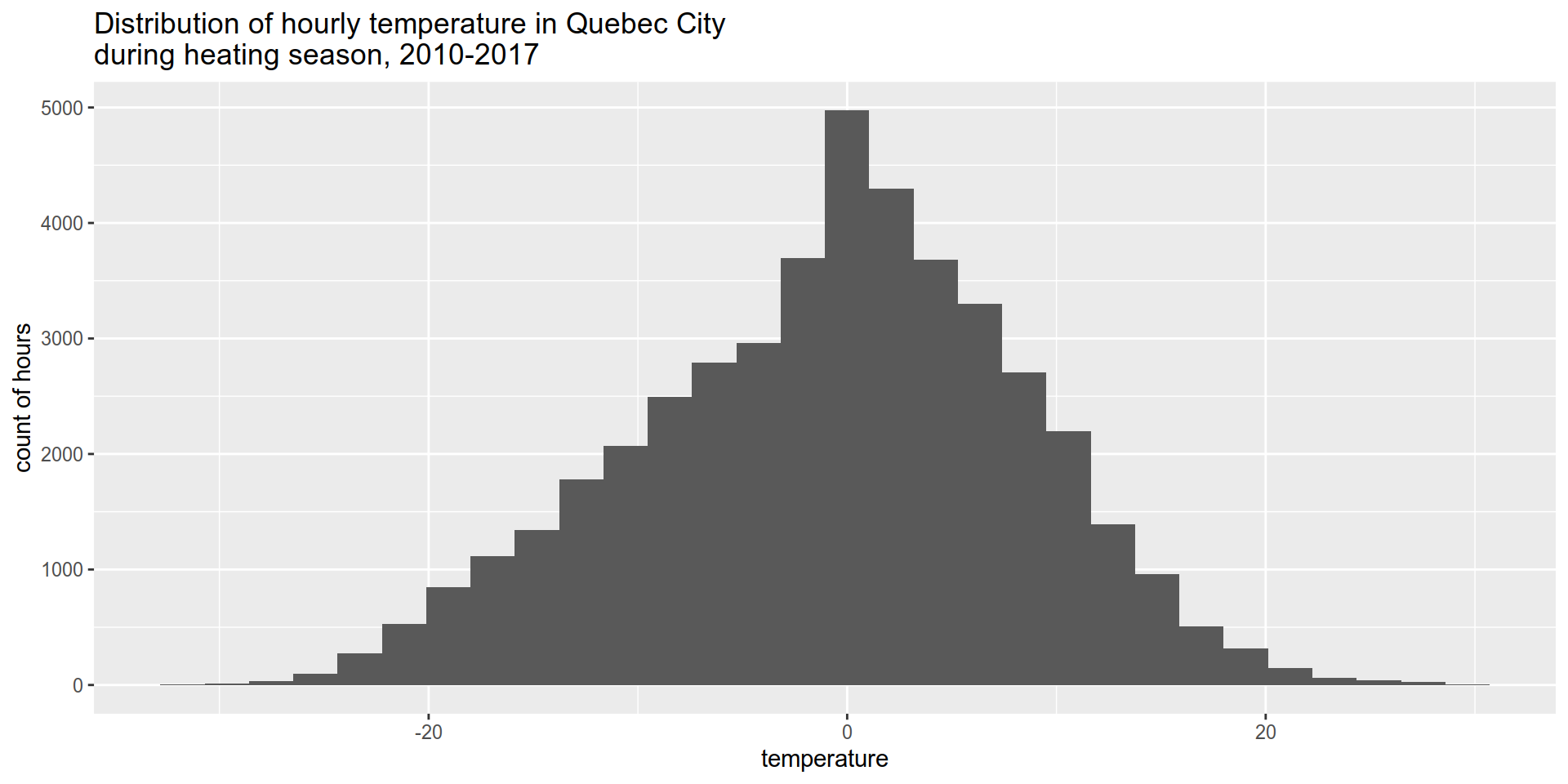
- As the outside temperature drops, the capacity of the heatpump will drop while the heating needs of your house increases. If the heat pump can’t provide enough heat, you must switch it off and use the backup system instead.
Economic objective
The heat pump and a new 15 kW electric furnace will cost me 7500$ after taxes and subsidies. The net cost of upgrading from an air conditioner to a heat pump is not clear and I ended up never getting a quote for only the central air conditioner. For argument’s sake let’s say that it’s about 4000 $. The heat pump is warrantied parts and labor for 10 years, so we will assume that it will work without maintenance for 10 years, then stop working.
A rule of thumb is that heating represents about 50-60% of a house’s electricity needs in Quebec. This is my first year in my house, but the former owners spent about 3000$ on electricity every year. We will assume that my heating costs are about 1800$ (60%) per year since my house is older with bad insulation.
Objective: I’ll be happy to break even if it means reducing my energy use.
To figure out my savings, I will need to generate a custom HSPF based on my local climate, my heat pump’s specification and my house’s energy needs.
Heat Pump efficiency and capacity
The technical sheet of the York heat pump gives us the efficiency and capacity of the heat pump for 6 temperatures. I need to know these values for all possible temperature, so I create two functions, get_COP and get_MBH that linearly interpolate the values.
I will assume that the heat pump stops working at the lowest temperature on the technical sheet (-12.2C). The quote I received says that it operates until -17C, but I haven’t seen that value in any official documentation.
Weather Data
Two things depend on the outside temperature: my house’s energy needs and the heat pump’s efficiency and capacity.
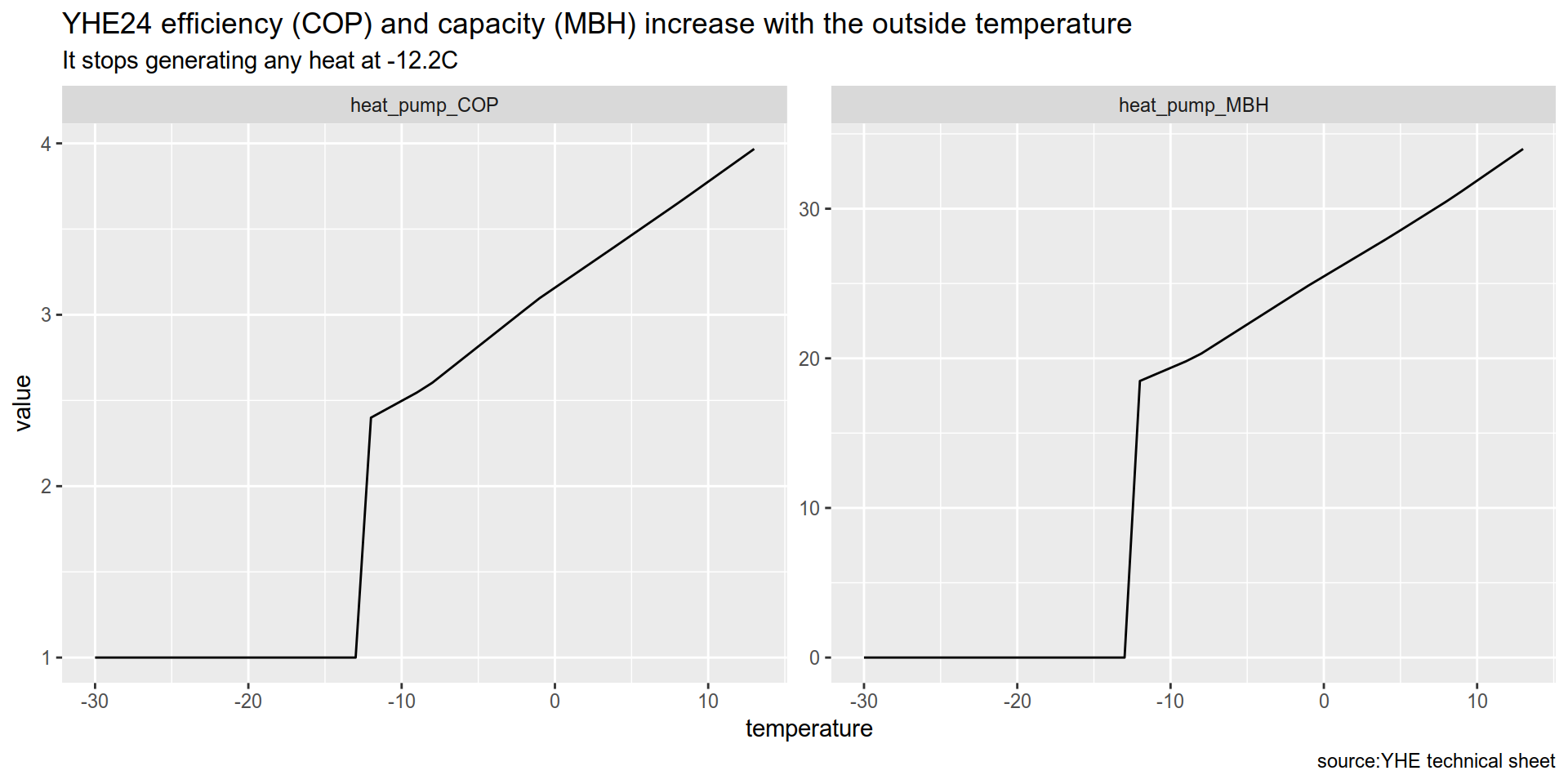
For this project, we will us rOpenSci’s weathercan package along the usual suspects from the tidyverse. Provided my longitude and latitude, the weathercanpackage will download the hourly temperature data for the closest local Environment Canada weather station.
It is important to use the hourly temperature rather than the daily average temperature when working with heat pumps For example, 12 hours at night at -16C and 12 hours during the day at 0C is not equivalent to 24 hours at -8C. In that scenario, the heat pump would shut down at night, but if you only looked at the daily average you would think that it worked for 24 hours.
House heating needs
To estimate the heating needs of my house at all temperatures, I have held the inside temperature of my house constant at 21 Celsius between November 3rd and November 20th 2018.
Hydro-Québec (my electricity provided) uses smart meters, so I can now download a .csv with my hourly electricity consumption in kWh from my customer account. They have even added the outside temperature! I will use these two values to model my heating needs as a function of the outside temperature.
I argue that almost 100% of my electricity consumption goes to heating. For example, all the electricity used by my fridge, computer and light is eventually 100% converted into heat that my electric furnace won’t need to generate. The only electricity that is “wasted” is hot water, since that hot water is just flushed down the drain and doesnt warm up my house.
The biggest use of hot water is in the morning (adult shower) and evening (children bath), but hopefully that won’t break the model.
Thermodynamics state that my heating use should increase as a linear function of temperature. It appears to be true ( awesome!)

Let’s model the electricty consumption (proxy for heating needs) :
#
# Call:
# lm(formula = kWh ~ temperature, data = hydro %>% filter(date >=
# lubridate::ymd(start)))
#
# Coefficients:
# (Intercept) temperature
# 4.2475 -0.1599Putting it all together
We can finally combine all the sources. For each hour during the heating seasons between 2010 and 2017, we will figure out my house’s energy needs. We will then look at the heat pump’s capacity and efficiency to figure out which system will be used (heat pump or backup). Knowing which system is in use, we will estimate my house’s energy needs for that hour.
We are then be able to calculate the coefficient of performance the heat pump would have had for each year.
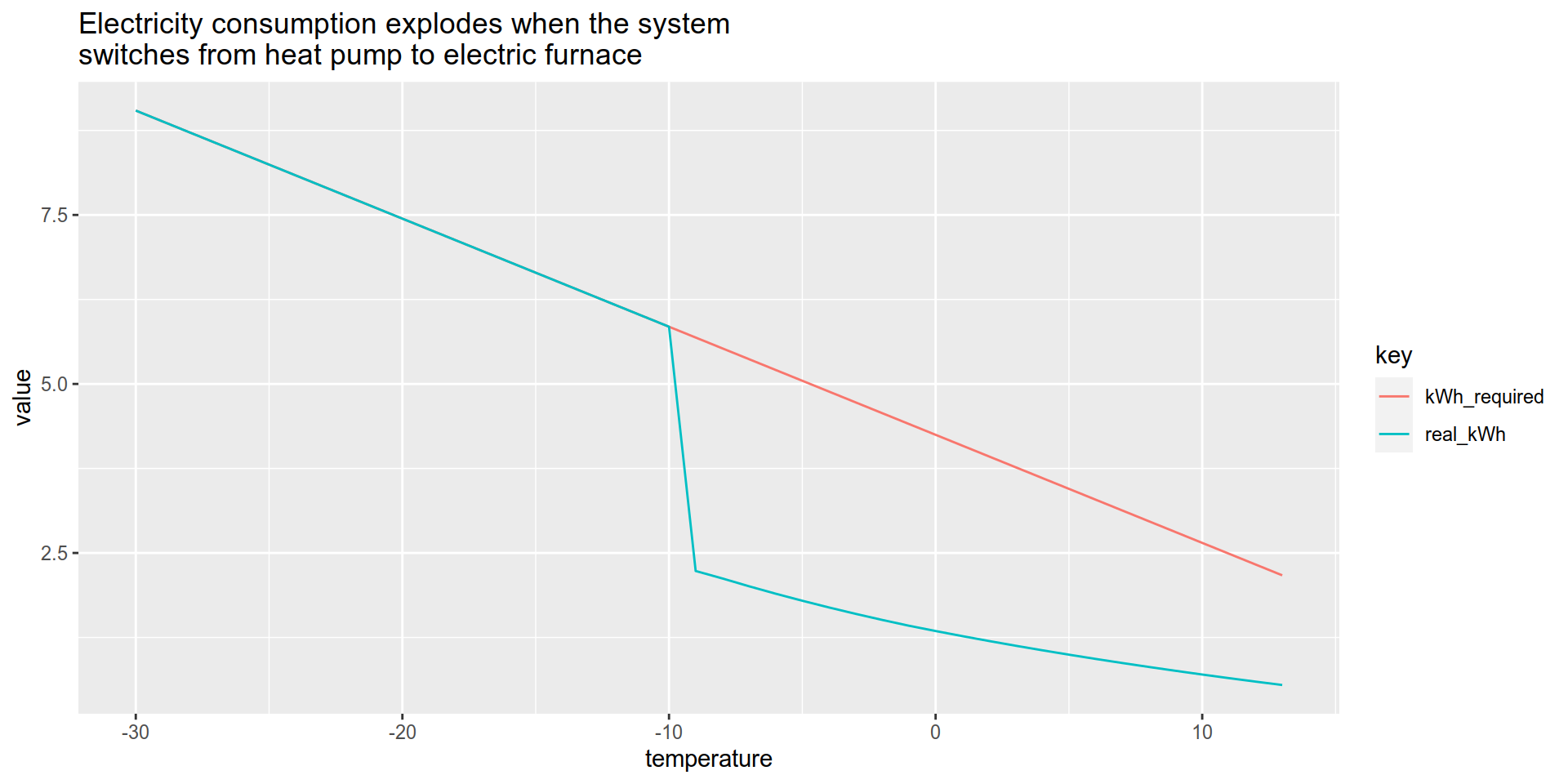
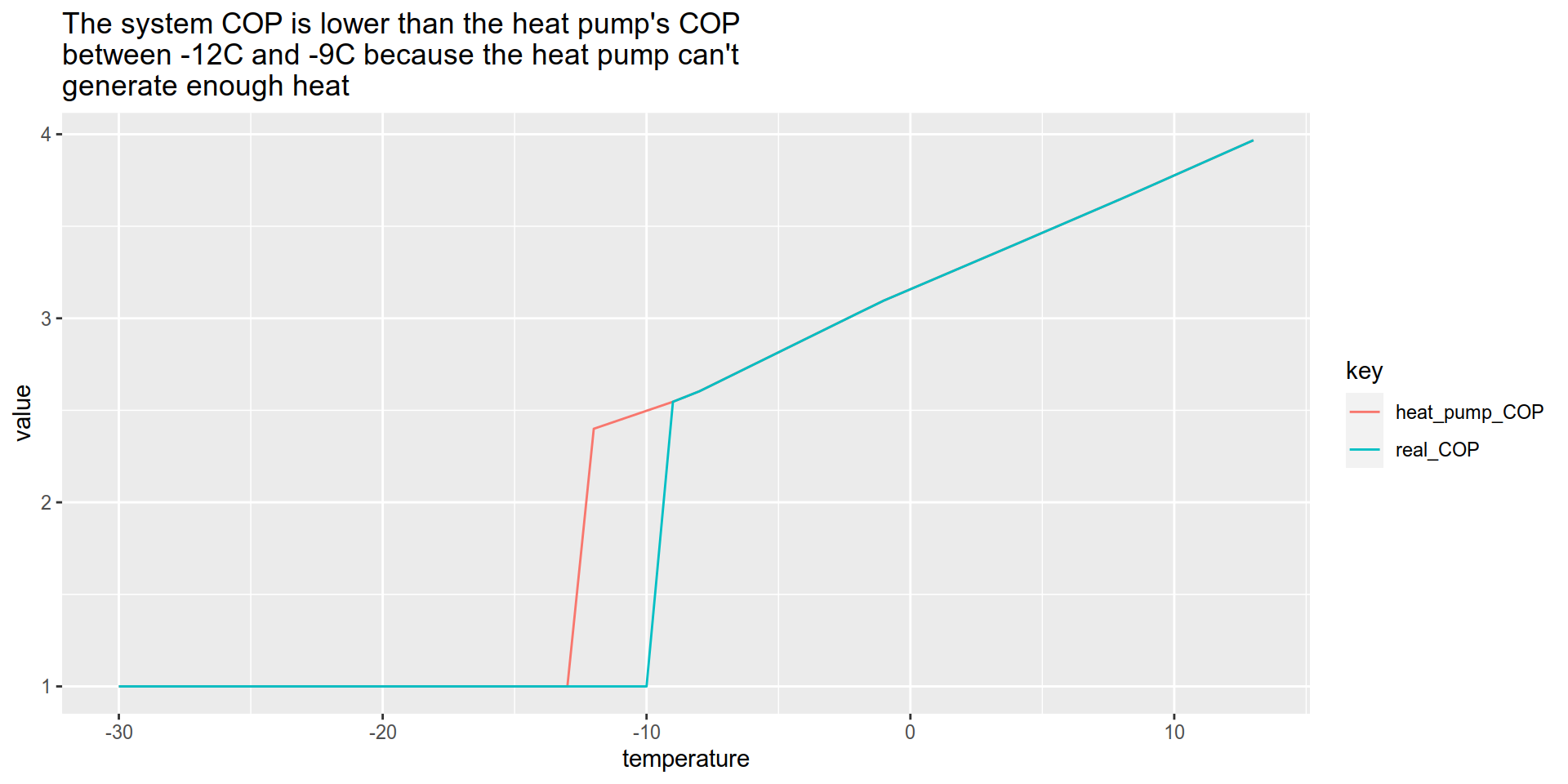
Conclusion
The table below summarise the findings.
First, a sanity check: the model predicts that I am currently spending about 1708$ per year on average on heating if I do not change anything. This is 57% of my total electricity bill, which fits right inside the rule of thumb we mentionned earlier.
My local adjusted COP of 1.97 is slightly lower than the published COP of 2.16, which is expected since my region is colder than Ottawa. The savings of 804$ represent 49% of my predicted heating bill and 26.8% of my total electricity bill.
This is hopefully a realistic estimate. One one side, I was optimist and assumed that 100% of my electricity bill is heating, which means that I assume that all my electricity consumption can be reduced by the heat pump. This is obviously not true, since my fridge energy use won’t be reduced by the heat pump. One the other side, I was pessimist and assumed that my heat pump would stop working at -9C since it cant output enough energy to cover 100% of my electricity consumption. This is false for two reasons. First, my fridge still accounts for some of that electricity consumption. Second, I do have baseboard heaters scattered around the house, so the heat pump will probably be able to “output whatever it can do and let the baseboard do the rest”. This means that my COP will probably remain above 1 until -12C (tech sheet) or maybe even -17C (quote) instead of only until -9C.
Ignoring compounding interests (it is 2AM after all), the payback period on the extra 4000 $ I spend to get the heat pump over the air conditionning would only be 5 years. The remaining 5 years of life in the heat pump would be profit, or a cushion to protect against problems.
If I only bought the heat pump for the heating efficiency gains (7 500$), then the payback period would be almost 10 years, ignoring interests and maintenance. This is the expected life of the unit, and this wouldnt be economically viable.
Thus, it appears that getting the heat pump is a good idea if you were getting the air conditionning anyway, but is not a good idea if you were not.
Next step: buy the damn thing. It will be very interesting to model my energy consumption as a piecewise regression once I get my heat pump installed.
